Odds and Probability

Lead Author(s): Jeff Martin, MD

Odds = Probability of an Event

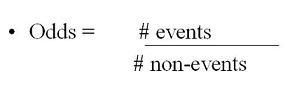Odds are most simply calculated as the number of events divided by the number of non-events.

The formal way to describe the odds is as the probability of the event divided by the probability of the non-event.

So odds are the ratio of two fractions:

the number of events divided by the number of subjects ( the probability of the event) and
that fraction divided by the number of non-events divided by the number of subjects ( the probability of the non-event).

So the formula for odds is p / (1 - p).

Since both fractions have the number of subjects in the denominator,

they reduce to our first presentation of odds as the number of events divided by the number of non-events.

If event occurs 1 of 5 times, probability = 0.2

Out of 5 times, 1 time will be the event and 4 times will be the non-event, odds = 0.25

Calculating the odds without the number of subjects:

To calculate probability given the odds:

Probability = odds/1+ odds To go in the other direction from odds to probability:
Divide the odds by 1 + odds.
In this example, (1/4) / (1+1/4) =
(1/4) / (5/4) =
1/5, the probability

Odds is less intuitive than probability (probably wouldn't say "my odds of dying are 1/4")

No less legitimate mathematically, just not so easily understood

Also important because the log odds of the outcome is given by the coefficient of a predictor in a logistic regression

In multivariate analysis of a dichotomous outcome logistic regression is used and the coefficients, the betas, from a logistic regression give the odds ratio by raising e to the beta (exponentiating it on the natural logarithm scale).